June 4, 2009
Invisibility research has led to discovery of ‘wormholes’
Three years ago, mathematicians in the United States and Great Britain announced the discovery of an invisibility cloak. Yes, you read that right, they calculated the properties for a material that guides light rays around an object so there appears to be nothing there.
Now UW mathematics professor Gunther Uhlmann, part of that original research, has taken it a step further — he has discovered an electromagnetic “wormhole,” a tunnel that would make light waves seem to disappear in one place and reappear somewhere else.
We’re still waiting to see invisibility capes for sale at the local Toys ‘R Us. But the past three years have seen the birth of a new field in invisibility. Wormholes and invisibility cloaks, once the stuff of legend, are now a subject of serious research.
Uhlmann has been closely involved since before day one. He and his collaborators originally solved the equations to redirect rays years ago while using waves to detect breast-cancer tumors. See our earlier story on the unexpected discovery.
The prospect of invisibility prompted Uhlmann and colleagues to revisit their original equations, with some intriguing results. A little more than a year ago Uhlmann and co-authors published a high-profile paper announcing their discovery of an electromagnetic wormhole. Their wormhole, named after a concept in general relativity, is a tunnel that would make light waves seem to disappear in one place and reappear somewhere else.
“The idea is to create a tunnel of invisibility, a secret connection between two different points in space,” Uhlmann said.
He started to work on the wormhole idea almost immediately after the cloak was announced. It takes the invisibility concept from one dimension to two dimensions.
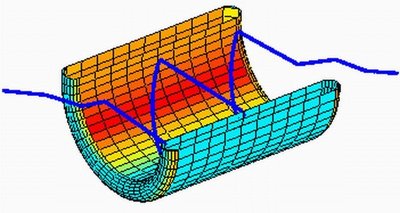
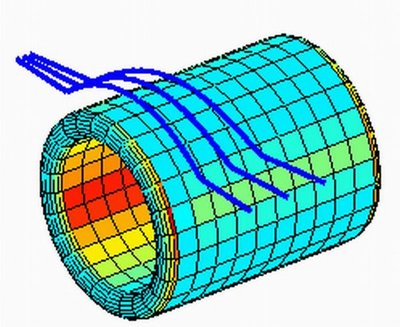
“The previous work came from blowing up a point,” Uhlmann explained. “The wormhole comes from blowing up a line.” Co-authors of the paper published in Physical Review Letters in October 2007 are, in alphabetical order, Allan Greenleaf of the University of Rochester, Yaroslav Kurylev at University College London and Matti Lassas at the University of Helsinki.
The wormhole is like all invisibility work so far in that it hides only specific frequencies — in this case, those in the electromagnetic range. The mathematicians solved equations that show the path that rays would take through this object and the characteristics of the material that would create the tunnel.
By Gunther Uhlmann When sound waves move through space, or water waves move across the surface of the ocean, the loudness of the sound and the height of the water change in ways that can be predicted using mathematics. In the same way, when light or cell phone signals move through space, they travel as waves and the way they change can be predicted. It is useful to invent devices that change the way light travels. For example, the glass in the lenses of a pair of eyeglasses are made out of glass or plastic that has been designed to bend the light waves a little to correct for problems in the shape of the natural lenses in the person’s eyes. The “electromagnetic wormhole” is a design for an extreme kind of optical device, which tricks the light waves into behaving as though they are moving through a space which has a different shape from the one we actually live in. To get an idea of what this means, think of ants marching across a flat surface, such as a wall. Now compare that with ants walking on the front of a dresser with pull-out handles. When an ant comes to a handle, it can either stay on the flat part of the dresser front, or it can travel along the curved handle, which is like a bridge or tunnel, and eventually walk out back onto the flat surface. Another ant can at the same time walk between the handle and the flat surface, and neither ant will know that the other one is there. The electromagnetic wormhole does essentially the same thing for light or radio waves. |
The wormhole discovery was covered in Nature, Scientific American and National Geographic.
Now the major challenge is to build a prototype.
“The mathematics of cloaking, the basic things, are known,” Uhlmann says. “The main thing now is: How do you build the materials that are required?”
The solutions to the equations require that the cloak be made from metamaterials, which are materials that have properties beyond those of any found in nature. Examples of metamaterials that would work for cloaking are ones with a negative index of refraction, which until recently was thought impossible.
The materials must be built at the nano-scale because they are constructed to match the incoming waves, Uhlmann says. The longer the wavelength the easier it is to build. That explains why the first working cloak, immortalized in a YouTube video, hid a copper cylinder from microwaves with wavelengths more than a thousand times longer than those of visible light.
“Recently there have been experiments done for higher frequencies, getting closer and closer to visible light,” Uhlmann said.
To make the materials required to cloak visible light, Uhlmann believes there needs to be more communications between mathematicians and engineers. For that reason he and his collaborators have been publishing in journals such as Physical Review Letters and Optics Express rather than in mathematics journals.
In a similar spirit of collaboration, Uhlmann organized a conference last fall at the University of Maryland that brought together mathematicians and engineers to work on invisibility materials. In January he will attend a similar meeting at the University of California at Los Angeles. Uhlmann also plans to devote an upcoming sabbatical to working with engineers to actually build the materials required by these invisibility equations.
Meanwhile, Uhlmann is involved in other projects related to the mathematical basis of invisibility. He is working on a paper on partial invisibility, in which an object would be almost invisible, but would have some communication with the outside world. With the existing technology anything hidden inside the cloak or wormhole can’t see out.
A postdoctoral researcher working with Uhlmann, Hongyu Liu, published a paper showing that a wall could be made to appear when there is actually nothing there.
“It all comes from the same idea,” Uhlmann says. “Making things expand and contract, making things look different things than what they really are.”
The mathematics of invisibility cloaks and wormholes builds on Uhlmann’s decades of expertise in inverse problems, using wave behavior to deduce an object’s internal structure. When Uhlmann was recently named a fellow of the American Academy for Arts and Sciences the award citation recognized both his recent invisibility research and his previous work on inverse problems. But to the average person, Uhlmann admits, the word “invisibility” sparks more interest than the phrase “inverse problems.”
Uhlmann is one of the investigators on a $2 million Research Training Grant from the National Science Foundation awarded to the UW’s Department of Mathematics for work on partial differential equations and inverse problems. Some of this grant will fund more graduate students and post-docs to work on partial differential equations and inverse problems, including various aspects of invisibility research.
“Like anything in science, some people say it won’t be possible,” Uhlmann says. “But I think that for limited frequencies, it might very well be possible. There has been a lot of progress already.”